Karnaugh Map atau yang biasanya disebut dengan K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.
Rumus untuk menentukan jumlah kotak pada K-Map adalah 2n n adalah banyaknya variabel / inputan.
Langkah – langkah pemetaan K-Map secara umum :
- Menyusun aljabar Boolean terlebih dahulu
- Menggambar rangkaian digital
- Membuat Table Kebenarannya
- Merumuskan tabel kebenaran
- Lalu memasukkan rumus Tabel Kebenaran ke K-Map (Kotak-kotak
Penyederhanaan Dua Variabel
Catatan : Bar = ‘
Tabel dari K-Map 2 variabel adalah seperti dibawah ini
Contoh Soal
H = AB + A’B+AB’
H = AB + A’B+AB’
Maka cara pengerjaanya seperti dibawah ini
Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘
Dan dapat dipermudah lagi menjadi dibawah ini
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya
Yaitu terletak pada kotak 01 + 11 dan 10 + 11 yaitu cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A dan B.
Caranya :
01
11
1 yang sama adalah angka 1 yang dibelakang jadi jika letaknya dibelakang (kedua) adalah B (B diambil dari tabel K-Map Diatas ) jika yang sama angka 0 pada urutan kedua adalah B’ diatas sudah disebutkan bahwa angka 0 = Bar/’
10
11
1 yang sama adalah angka 1 yang didepan jadi jika letaknya didepan (pertama) adalah A (A diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ diatas sudah disebutkan bahwa angka 0 = Bar/’
Jadi kesimpulan dari contoh diatas adalah dari rumus :
H = AB + A’B + AB’ dapat disederhanakan menggunakan K-Map menjadi
BA / AB (boleh dibalik menurut abjad tetapi harus 1 teman atau tidak dapat dibalik dengan huruf yang dipisahkan dengan penjumlahan atau pengurangan)
Penyederhanaan Tiga Variabel
Catatan : Bar = ‘
Tabel dari K-Map 3 variabel adalah seperti dibawah ini
Contoh Soal
H = ABC + A’BC+A’B’C+AB’C
H = ABC + A’BC+A’B’C+AB’C
Maka cara pengerjaanya seperti dibawah ini
Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘
Dan dapat dipermudah lagi menjadi dibawah ini
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya
Cara diatas adalah langsung mesederhanakan 4 kotak, sebenarnya dapat disederhanakan menjadi 2 kotak 2 kotak tetapi terlalu lama dan kita hanya menyingkat waktu saja menjadi 4 kotak langsung, terletak pada kotak 001 + 011+101 +111 yaitu cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A, B, C.
Caranya :
011
011
101
111
1 yang sama adalah angka 1 yang dibelakang jadi jika letaknya dibelakang (keempat) adalah C (C diambil dari tabel K-Map Diatas ). Jika yang sama angka 0 pada urutan keempat adalah C’ diatas sudah disebutkan bahwa angka 0 = Bar/’
Jadi kesimpulan dari contoh diatas adalah dari rumus :
H = ABC + A’BC+A’B’C+AB’C dapat disederhanakan menggunakan K-Map menjadi C.
Penyederhanaan 4 variabel
Catatan : Bar = ‘
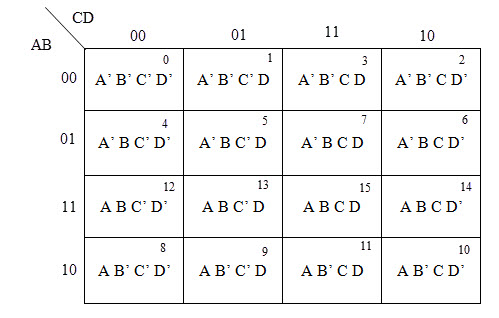
Tabel dari K-Map 4 variabel adalah seperti dibawah ini
Contoh Soal
H = ABCD + ABCD’+AB’CD+ABC’D’
H = ABCD + ABCD’+AB’CD+ABC’D’
Maka cara pengerjaanya seperti dibawah ini
Bar / ‘ biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar / ‘
Dan dapat dipermudah lagi menjadi dibawah ini
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya
Yaitu terletak pada kotak 1111 + 1011 dan 1111 + 1110 dan 1110 + 1100. Cara diatas menyederhanakannya dapat dari sisi paling kanan dengan sisi paling kiri dalam 1 baris.
Cara penyederhanaan dengan cara menulis angka yang sama (1 lingkaran) dan menerjemahkannya kedalam bentuk huruf seperti A, B, C, D.
Caranya :
1111
1011
1 11 yang sama adalah angka 1 yang pertama, ketiga, dan keempat adalah A, C, dan D (A, C, dan D diambil dari tabel K-Map Diatas ) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’
1111
1110
111 yang sama adalah angka 1 yang pertama, kedua, dan ketiga adalah A, B, C (A, B, C diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’
1110
1100
11 yang sama adalah angka 1 yang pertama dan kedua adalah A dan B (A dan B diambil dari tabel K-Map Diatas) jika yang sama angka 0 pada urutan kedua adalah A’ dst diatas sudah disebutkan bahwa angka 0 = Bar/’
Jadi kesimpulan dari contoh diatas adalah dari rumus :
H = AB + A’B + AB’ dapat disederhanakan menggunakan K-Map menjadi
ACD + ABC + AB (boleh dibalik menurut abjad tetapi harus 1 teman atau tidak dapat dibalik dengan huruf yang dipisahkan dengan penjumlahan atau pengurangan)
Aljabar Bolean
Aljabar Boolean dapat didefinisikan dalam beberapa cara. Cara yang paling umum adalah dengan menspesifikasikan unsur – unsur pembentuknya dan operasi – operasi yang menyertainya.
Misalkan B adalah himpunan yang didefinisikan pada dua operator biner, + dan ., dan sebuah operator uner,’. Misalkan 0 dan 1 adalah dua elemen yang berbeda dari B. Maka, tupel <B, +, ., ‘, 0, 1> disebut aljabar Boolean jika untuk setiap a, b, c 0 B berlaku aksioma berikut :
1. Identitas
(i) a + 0 = a
(ii) a . 1 = a
2. Komutatif
(i) a + b = b + a
(ii) a . b = b . a
3. Distributif
(i) a . (b + c) = (a . b) + (a . c)
(ii) a + (b . c) = (a + b) . (a + c)
4. Komplemen
Untuk setiap a 0 B terdapat elemen unik a’ 0 B sehingga
(i) a + a’ = 1
(ii) a . a’ = 0
5. Closure: (i) a + b E B (ii) a × b E B
Angka 0 dan 1 adalah dua elemen yang berada di dalam B. 0 disebut
elemen terkecil dan 1 disebut elemen terbesar. Tanda (+) disebut operator penjumlahan,( .) disebut operator perkalian, dan ( ‘) disebut operator komplemen.
Ada perbedaan antara aljabar Boolean dengan aljabar biasa untuk aritmetika bilangan riil :
1. Hukum distributif yang pertama, a . (b + c) = (a . b) + (a . c) sudah dikenal di dalam aljabar biasa, tetapi hukum distributif yang kedua, a + (b . c) = (a + b) . (a + c)
2. Aljabar Boolean tidak memiliki kebalikan perkalian dan kebalikan penjumlahan; karena itu, tidak ada operasi pembagian dan pengurangan di dalam aljabar Boolean.
3. Aljabar biasa memperlakukan himpunan bilangan riil dengan elemen yang tidak berhingga banyaknya.
Aljabar Boolean dua-nilai:
- B = {0, 1}
- operator biner, + dan ×
- operator uner, ’
- Kaidah untuk operator biner dan operator uner:
a
|
b
|
a × b
|
a
|
b
|
a + b
|
a
|
a’
| ||
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
| ||
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
| ||
1
|
0
|
0
|
1
|
0
|
1
| ||||
1
|
1
|
1
|
1
|
1
|
1
|
Buktikan apakah memenuhi postulat Huntington:
1. Closure : berlaku
2. Identitas: berlaku karena dari tabel dapat di lihat bahwa:
(i) 0 + 1 = 1 + 0 = 1
(ii) 1 × 0 = 0 × 1 = 0
3. Komutatif: berlaku dengan melihat simetri tabel operator biner.
4. Distributif: (i) a × (b + c) = (a × b) + (a × c) dapat ditunjukkan benar dari tabel operator biner di atas dengan membentuk tabel kebenaran
5. Komplemen: jelas berlaku karena memperlihatkan bahwa:
(i) a + a‘ = 1, karena 0 + 0’= 0 + 1 = 1 dan 1 + 1’= 1 + 0 = 1
(ii) a × a’ = 0, karena 0 × 0’= 0 × 1 = 0 dan 1 × 1’ = 1 × 0 = 0
Kesimpulannya: Karena kelima postulat Huntington dipenuhi, maka terbukti bahwa B = {0, 1}
Ekspresi Boolean
- Semisal (B, +, ×, ’) sebuah aljabar Boolean.
- Suatu ekspresi Boolean dalam (B, +, ×, ’) dapat berbentuk:
(1) elemen di dalam B, ex : 0 dan 1
(2) peubah/ literal/ variable, ex : a, b, c
(3) jika e1 dan e2 adalah ekspresi Boolean, maka e1 + e2,
e1 × e2, e1’ adalah ekspresi Boolean
Prinsip Dualitas
Semisal S kesamaan di dalam aljabar Boolean yang menggunakan operator +, ×, dan komplemen, maka jika pernyataan S* diperoleh dengan cara mengganti
× dengan +
+ dengan ×
0 dengan 1
1 dengan 0
dan biarkan operator komplemen tetap apa adanya, maka kesamaan S* juga benar.
Contoh.
(1) (a × 1)(0 + a’) = 0 dualnya (a + 0) + (1 × a’) = 1
(2) a(a‘ + b) = ab dualnya a + a‘b = a + b
1. Cara pertama: menggunakan hukum De Morgan
Hukum De Morgan untuk dua buah peubah, x1 dan x2, adalah
Contoh. Semisal f(x, y, z) = x(y’z’ + yz), maka
f ’(x, y, z) = (x(y’z’ + yz))’
= x’ + (y’z’ + yz)’
= x’ + (y’z’)’ (yz)’
= x’ + (y + z) (y’ + z’)
2. Cara kedua: menggunakan prinsip dualitas.
Tentukan dual dari ekspresi Boolean yang merepresentasikan f, lalu komplemenkan setiap literal di dalam dual tersebut.
Bentuk Kanonik
· Jadi, ada dua macam bentuk kanonik:
1. Penjumlahan dari hasil kali (sum-of-product atau SOP)
2. Perkalian dari hasil jumlah (product-of-sum atau POS)
Contoh: 1. f(x, y, z) = x’y’z + xy’z’ + xyz --> SOP
Setiap suku (term) disebut minterm
2. g(x, y, z) = (x + y + z)(x + y’ + z)(x + y’ + z’)
(x’ + y + z’)(x’ + y’ + z) --> POS
Setiap suku (term) disebut maxterm
- Setiap minterm/maxterm mengandung literal lengkap
Minterm
|
Maxterm
| |||||
x
|
y
|
Suku
|
Lambang
|
Suku
|
Lambang
| |
0
0
1
1
|
0
1
0
1
|
x’y’
x’y
xy’
x y
|
m0
m1
m2
m3
|
x + y
x + y’
x’ + y
x’ + y’
|
M0
M1
M2
M3
| |
Contoh.
buatlah tabel kebenaran di bawah ini dalam bentuk kanonik SOP dan POS.
Tabel
x
|
y
|
z
|
f(x, y, z)
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
0
0
1
0
0
1
|
Jwab:
(a) SOP
Perpaduan nilai-nilai peubah yang menghasilkan nilai fungsi sama dengan 1 adalah 001, 100, dan 111, maka fungsi Booleannya dalam bentuk kanonik SOP:
f(x, y, z) = x’y’z + xy’z’ + xyz
atau bisa (dengan menggunakan lambang minterm),
f(x, y, z) = m1 + m4 + m7 = (1, 4, 7)
(b) POS
Kombinasi nilai-nilai peubah yang menghasilkan nilai fungsi sama dengan 0 adalah 000, 010, 011, 101, dan 110, maka fungsi Booleannya dalam bentuk kanonik POS adalah
f(x, y, z) = (x + y + z)(x + y’+ z)(x + y’+ z’)
(x’+ y + z’)(x’+ y’+ z)
atau dalam bentuk lain,
f(x, y, z) = M0 M2 M3 M5 M6 = (0, 2, 3, 5, 6)